SHOW THAT : 2^(2N) – 3N -1 is divisible by 9 FOR ALL N>=1
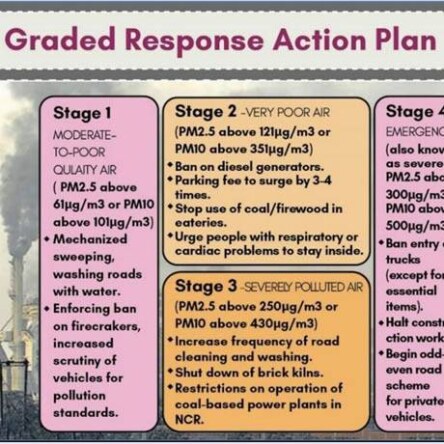
GRAP Stage 3 entails a ban on non-essential construction work. Classes up to grade V are required to shift to hybrid mode under Stage 3. Parents and students have the option to choose online education wherever available. Under Stage 3, the use of BS-III petrol and BS-IV diesel cars (4-wheelers) is rRead more
GRAP Stage 3 entails a ban on non-essential construction work. Classes up to grade V are required to shift to hybrid mode under Stage 3. Parents and students have the option to choose online education wherever available.
Under Stage 3, the use of BS-III petrol and BS-IV diesel cars (4-wheelers) is restricted in Delhi and nearby NCR districts. Persons with disabilities are exempt.
Stage 3 also bans non-essential diesel-operated medium goods vehicles with BS-IV or older standards in Delhi. The Stage 3 of GRAP was lifted on December 27 after a marked improvement in Delhi’s air quality following day-long rainfall in the national capital.
Throughout 2024, Delhi recorded the highest number of ‘severe’ AQI days since 2022, with 17 days exceeding an AQI of 400. Additionally, 70 days were classified as ‘very poor’. Not a single ‘good’ air quality day was recorded in 2024, a first since 2018.
See less
Proof by Mathematical Induction: Base Case: Let \( n = 1 \) \[ 2^{2 \cdot 1} - 3 \cdot 1 - 1 = 2^2 - 3 - 1 = 4 - 3 - 1 = 0 \] \[ \Rightarrow 9 \mid 0 \quad \text{(True)} \] Inductive Hypothesis: Assume that for some \( n = k \), the expression is divisible by 9: \[ 2^{2k} - 3k - 1 \equiv 0 \pmod{9}Read more
Proof by Mathematical Induction:
Base Case: Let \( n = 1 \)
\[
2^{2 \cdot 1} – 3 \cdot 1 – 1 = 2^2 – 3 – 1 = 4 – 3 – 1 = 0
\]
\[
\Rightarrow 9 \mid 0 \quad \text{(True)}
\]
Inductive Hypothesis: Assume that for some \( n = k \), the expression is divisible by 9:
\[
2^{2k} – 3k – 1 \equiv 0 \pmod{9}
\]
That is,
\[
2^{2k} – 3k – 1 = 9m \quad \text{for some integer } m
\]
To Prove: \( 2^{2(k+1)} – 3(k+1) – 1 \) is also divisible by 9.
LHS:
\[
2^{2(k+1)} – 3(k+1) – 1 = 2^{2k + 2} – 3k – 3 – 1
\]
\[
= 4 \cdot 2^{2k} – 3k – 4
\]
Now subtract the inductive hypothesis:
\[
[4 \cdot 2^{2k} – 3k – 4] – [2^{2k} – 3k – 1] = 3 \cdot 2^{2k} – 3
\]
\[
= 3(2^{2k} – 1)
\]
Now, observe that \( 2^{2k} \equiv 1 \pmod{3} \), so \( 2^{2k} – 1 \equiv 0 \pmod{3} \)
Hence, \( 3(2^{2k} – 1) \equiv 0 \pmod{9} \)
Therefore, the expression for \( n = k+1 \) is also divisible by 9.
Conclusion:
\[
See less\boxed{2^{2n} – 3n – 1 \text{ is divisible by } 9 \text{ for all } n \geq 1}
\]